Intro to Item Response Modeling in R

An Tutorial on MIRT Package

Jan 1, 0001

Overview

The goal of this document is to introduce applications of R for item response theory (IRT) modeling. Specifically, this document is focused on introducing basic IRT analyses for beginners using the “mirt” package (Chalmers, 2012). It is not intended to be a full introduction to data analysis in R, nor to basic mathematics of item response theory. Instead, this tutorial will introduce the key concepts of IRT and important features of corresponding R packages/functions that facilitate IRT modeling for beginners. For a quick reference on the basics of IRT, please see the last section of recommended readings.

In this tutorial, we will focus on unidimensional IRT models by presenting brief R examples using “mirt”. Specifically, we will talk about:
1. Key concepts in IRT;
2. Dichotomous, 1PL Model (Rasch Model);
3. Dichotomous, 2PL Model;
4. Polytomous, Generalized Partial Credit Model.

Install and Load Packages

The first step is to make sure you have the R packages needed in this tutorial. We can obtain the “mirt” package from CRAN (using “install.packages(‘mirt’)”), or install the development version of the package from Github using the following codes:

install.packages('devtools')
library('devtools')
install_github('philchalmers/mirt')

We need the following packages in this tutorial:

library(tidyverse) # For data wrangling and basic visualizations
library(psych) # For descriptive stats and assumption checks
library(mirt) # IRT modeling

Prepare the Data

The next step is to read in and prepare corresponding data files for the tutorial. The two data files we are using in this tutorial are available at here: ReadingSpan and RotationSpan.

These two datasets consist of item-level responses from 261 subjects on 2 complex span tasks: reading span and rotation span. In a complex span task, each item has a varying number of elements to process and memorize (item size). The responses in the two datasets are integer numbers that reflect the numbers of correctly recalled elements for each item. For the reading span task, there are 15 items presented across 3 blocks, with item sizes varied from 3 to 7. For the rotation span task, there are 12 items presented across 3 blocks, with item sizes varied from 2 to 5.

# Conway et al. (2019) Data
wmir <- read.csv("WMI_Read_Han_wide.csv")[,-1]
wmirot <- read.csv("WMI_Rot_Han_wide.csv")[,-1]

colnames(wmir) <- c("Subject", 
                   "V1.3", "V1.4","V1.5", "V1.6", "V1.7",
                   "V2.3", "V2.4","V2.5", "V2.6", "V2.7",
                   "V3.3", "V3.4","V3.5", "V3.6", "V3.7")

colnames(wmirot) <- c("Subject", 
                   "S1.2","S1.3", "S1.4","S1.5", 
                   "S2.2","S2.3", "S2.4","S2.5", 
                   "S3.2","S3.3", "S3.4","S3.5")


# Wmi is the full dataset (N = 261)
wmi <- merge(wmir, wmirot, by = "Subject")

head(wmir)

##   Subject V1.3 V1.4 V1.5 V1.6 V1.7 V2.3 V2.4 V2.5 V2.6 V2.7 V3.3 V3.4 V3.5 V3.6
## 1       1    3    4    5    2    3    3    4    2    2    1    1    2    4    0
## 2       2    3    2    5    6    6    3    3    3    4    7    3    3    5    6
## 3       3    3    4    3    6    6    3    4    5    3    4    3    4    5    5
## 4       4    2    2    2    2    3    3    2    2    0    0    3    4    5    2
## 5       5    3    3    3    4    7    3    4    5    6    5    3    1    5    6
## 6       6    3    4    4    6    2    3    4    5    6    2    3    4    4    6
##   V3.7
## 1    3
## 2    7
## 3    2
## 4    1
## 5    7
## 6    7

head(wmirot)

##   Subject S1.2 S1.3 S1.4 S1.5 S2.2 S2.3 S2.4 S2.5 S3.2 S3.3 S3.4 S3.5
## 1       1    2    1    0    0    0    3    1    0    1    1    0    0
## 2       2    2    2    1    1    2    3    2    2    2    2    1    1
## 3       3    2    1    4    1    2    3    4    1    1    2    0    3
## 4       4    2    2    3    1    2    0    1    1    2    2    3    4
## 5       5    2    3    4    5    2    3    4    4    2    3    4    2
## 6       7    2    3    0    2    2    3    4    3    2    1    2    1

Labels of the variables in the datasets indicate the corresponding block and item size of a specific item. For example, in the reading span dataset (wmir), the 5th column (“V1.6”) presents subjects’ responses on the item with 6 elements in the 1st block. Subject 1 recalled 2 of the 6 elements correctly.

For a detail summary of the two complex span tasks, see Conway et al. (2005) and Hao & Conway (2021).

Key Concepts in Item Response Theory

In this section we will briefly go over some key concepts and terms we will be using in this IRT tutorial.

Scale: In this tutorial, a scale refers to any quantitative system that is designed to reflect an individual’s standing or level of ability on a latent construct or latent trait. A scale consists of multiple manifest items. These items can be questions in a survey, problems in a test, or trials in an experiment.
- Dichotomous IRT models are applied to the items with two possible response categories (yes/no, correct/incorrect, etc.)
- Polytomous IRT models are applicable if the items have more than two possible response categories (Likert-type response scale, questions with partial credits, etc.)

Dimensionality: The number of distinguishable attributes that a scale reflect.
- For unidimensional IRT models, it is assumed that the scale only reflect one dimension, such that all items in the scale are assumed to reflect a unitary latent trait.
- For multidimensional IRT models, multiple dimensions can be reflected and estimated, such that the responses to the items in the scales are assumed to reflect properties of multiple latent traits.

Theta (\(\Theta\)): the latent construct or trait that is measured by the scale. It represents individual differences on the latent construct being measured.

Information: an index to characterize the precision of measurement of the item or the test on the underlying latent construct, with high information denoting more precision. In IRT, this index is represented as a function of persons at different levels, such that the information function reflects the range of trait level over which this item or this test is most useful for distinguishing among individuals.

Item Characteristic Curve (ICC): AKA item trace curve. ICC represents an item response function that models the relationship between a person’s probability for endorsing an item category (p) and the level on the construct measured by the scale (\(\Theta\)). For this purpose, the slope of the item characteristic curve is used to assess whether a specific item mean score has either a steeper curve (i.e., high value) or whether the item has a wider curve (i.e., low value) and, therefore, cannot adequately differentiate based on ability level.

Item Difficulty Parameter (b): the trait level on the latent scale where a person has a 50% chance of responding positively to the item. This definition of item difficulty applies to dichotomous models. For polytomous models, multiple threshold parameters (ds) are estimated for an item so that the latent trait difference between and beyond the response categories are accounted for.
- Conceptually, the role of item difficulty parameters in an IRT model is equivalent to the intercepts of manifests in a latent factor model.

Item Discrimination Parameter (a): how accurately a given item can differentiate individuals based on ability level. describes the strength of an item’s discrimination between people with trait levels below and above the threshold b. This parameter is also interpreted as describing how an item is related to the latent trait measured by the scale. In other words, the a parameter for an item reflects the magnitude of item reliability (how much the item is contributing to total score variance).
- Conceptually, the role of item discrimination parameters in an IRT model is equivalent to the factor loadings of manifests in a latent factor model.

The “mirt” package includes an interactive graphical interface (shiny app) to allow the parameters to be modified in an IRT exemplar item in real time. To facilitate understanding of these key concepts, you can run the line of code below in your R console to activate an interactive shiny app with examplar item trace plots for different types of IRT models.

itemplot(shiny = TRUE)

Unidimensional Dichotomous IRT Models

In this section we will start with the basic unidimensional dichotomous model, in which all items are assumed to measure one latent trait, and the responses to items are all binary (0 = incorrect/no, 1 = correct/yes). We will use the rotation span dataset (wmirot) in this section. As aforementioned, the raw data present numbers of correctly recalled elements for each item, which are not binary responses. Thus, we need to re-score these items using a all-or-nothing unit scoring approach (Conway et al., 2005; p.775), such that only a response with all elements in the item correctly recalled is scored as “correct” (1), while all other responses are scored as “incorrect” (0). The “mirt” package has a built-in function,“key2binary”, to assign binary scores to items in a dataset based on a given answer key. Thus, we can transfer all the initial rotation span responses to a binary response scale.

dat1 <- key2binary(wmirot[,-1],
    key = c(2,3,4,5,2,3,4,5,2,3,4,5))
head(dat1)

##      S1.2 S1.3 S1.4 S1.5 S2.2 S2.3 S2.4 S2.5 S3.2 S3.3 S3.4 S3.5
## [1,]    1    0    0    0    0    1    0    0    0    0    0    0
## [2,]    1    0    0    0    1    1    0    0    1    0    0    0
## [3,]    1    0    1    0    1    1    1    0    0    0    0    0
## [4,]    1    0    0    0    1    0    0    0    1    0    0    0
## [5,]    1    1    1    1    1    1    1    0    1    1    1    0
## [6,]    1    1    0    0    1    1    1    0    1    0    0    0

Assumption Checks

Unidimensional IRT models assume that all items are measuring a single continuous latent variable. There are different ways to test the unidimensionality assumption. For example, we can estimate McDonald’s hierarchical Omega (\(\omega_h\)), which conceptually reflects percentage of variance in the scale scores accounted for by a general factor. An arbitrary cutoff of \(\omega_h\) > .70 is usually used as the rule of thumb. Unfortunately, the current data violated this assumption using this rule of thumb (\(\omega_h\) = .56), but for demonstration purpose, we went along with further analyses.

For further details on unidimensionality, see Berge & Socan (2004) and Zinbarg, Yovel, Revelle, & McDonald (2006).

Another assumption of IRT is local independence, such that item responses are independent of one another. This assumption can be checked during the modeling fitting process by investigating the residuals and compute local dependence indices using the “residuals” function.

summary(omega(dat1, plot = F))

## Omega 
## omega(m = dat1, plot = F)
## Alpha:                 0.7 
## G.6:                   0.69 
## Omega Hierarchical:    0.56 
## Omega H asymptotic:    0.77 
## Omega Total            0.73 
## 
## With eigenvalues of:
##    g  F1*  F2*  F3* 
## 1.72 0.23 0.60 0.43 
## The degrees of freedom for the model is 33  and the fit was  0.07 
## The number of observations was  262  with Chi Square =  17.75  with prob <  0.99 
## 
## The root mean square of the residuals is  0.03 
## The df corrected root mean square of the residuals is  0.04 
## 
## RMSEA and the  0.9 confidence intervals are  0 0 0
## BIC =  -166.01Explained Common Variance of the general factor =  0.58 
## 
##  Total, General and Subset omega for each subset
##                                                  g  F1*  F2*  F3*
## Omega total for total scores and subscales    0.73 0.55 0.48 0.55
## Omega general for total scores and subscales  0.56 0.45 0.13 0.37
## Omega group for total scores and subscales    0.11 0.11 0.35 0.18

1PL (Rasch) Model

We can start with a 1PL (Rasch) model, in which the discrimination parameters for all items are fixed to 1, while difficulty paramters are freely estimated in the model.

# Model specification. Here we indicate that all columns in the dataset (1 to 12) measure the same latent factor ("rotation")
uniDich.model1 <- mirt.model("rotation = 1 - 12")

# Model estimation. Here we indicate that we are estimating a Rasch model, and standard errors for parameters are estimated.
uniDich.result1 <- mirt::mirt(dat1, uniDich.model1, itemtype = "Rasch", SE = TRUE)

Model and Item Fits

we can now investigate model fit statistics using the “M2” function, which provides the M2 index, the M2-based root mean square error of approximation (RMSEA), the standardized root mean square residual (SRMSR), and comparative fit index (CFI & TLI) to assess adequacy of model fit. A set of arbitrary cutoff values for the fit indices are provided here: RMSEA < .06; SRMSR < .08; CFI > .95; TLI > .95. Models with fit indices that saturate these cutoff values are commonly considered to have good fit. In this example, the non-significant M2 and all fit indices indicated great fit.

M2(uniDich.result1)

##             M2 df         p RMSEA RMSEA_5   RMSEA_95      SRMSR      TLI CFI
## stats 57.35425 65 0.7388256     0       0 0.02786492 0.05863013 1.016119   1

In IRT analyses, we can also assess how well each item fits the model. This is especially useful for item inspection and scale revision. The “itemfit” function provides S-X2 index as well as RMSEA values to assess the degree of item fit for each item. Non-significant S-X2 values and RMSEA < .06 are usually considered evidence of adequate fit for an item. In the current example, all items seem to fit the model well based on the indices.

itemfit(uniDich.result1)

##    item   S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
## 1  S1.2  7.250       5      0.042  0.203
## 2  S1.3 11.494       6      0.059  0.074
## 3  S1.4  7.566       6      0.032  0.272
## 4  S1.5  6.330       5      0.032  0.275
## 5  S2.2  4.483       6      0.000  0.612
## 6  S2.3  5.462       6      0.000  0.486
## 7  S2.4  5.275       6      0.000  0.509
## 8  S2.5  3.816       5      0.000  0.576
## 9  S3.2  1.528       6      0.000  0.958
## 10 S3.3  7.055       6      0.026  0.316
## 11 S3.4  5.081       6      0.000  0.533
## 12 S3.5  8.589       5      0.052  0.127

Along with the model and item fits we can also check the local independence assumption using the “residuals” function. The following scripts provide the LD matrix as well as dfs and p-values for all LD indices. Large and significant LD indices are indicators of potential issues of local dependence and may require further attention.

residuals(uniDich.result1, df.p = T)

## Degrees of freedom (lower triangle) and p-values:
## 
##      S1.2  S1.3  S1.4  S1.5  S2.2  S2.3  S2.4  S2.5  S3.2  S3.3  S3.4  S3.5
## S1.2   NA 0.812 0.572 0.317 0.736 0.537 0.572 0.038 0.228 0.142 0.224 0.302
## S1.3    1    NA 0.441 0.326 0.221 0.176 0.827 0.232 0.553 0.508 0.160 0.778
## S1.4    1 1.000    NA 0.833 0.077 0.643 0.414 0.248 0.694 0.237 0.412 0.482
## S1.5    1 1.000 1.000    NA 0.486 0.734 0.575 0.144 0.600 0.677 0.879 0.553
## S2.2    1 1.000 1.000 1.000    NA 0.741 0.758 0.214 0.233 0.084 0.770 0.214
## S2.3    1 1.000 1.000 1.000 1.000    NA 0.265 0.505 0.261 0.126 0.194 0.222
## S2.4    1 1.000 1.000 1.000 1.000 1.000    NA 0.429 0.694 0.534 0.063 0.248
## S2.5    1 1.000 1.000 1.000 1.000 1.000 1.000    NA 0.523 0.187 0.866 0.086
## S3.2    1 1.000 1.000 1.000 1.000 1.000 1.000 1.000    NA 0.151 0.774 0.872
## S3.3    1 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000    NA 0.352 0.717
## S3.4    1 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000    NA 0.156
## S3.5    1 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000    NA
## 
## LD matrix (lower triangle) and standardized values.
## 
## Upper triangle summary:
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  -0.128  -0.043  -0.014   0.000   0.060   0.109 
## 
##       S1.2   S1.3   S1.4   S1.5   S2.2   S2.3   S2.4   S2.5   S3.2   S3.3
## S1.2    NA -0.015 -0.035  0.062 -0.021 -0.038 -0.035 -0.128  0.074 -0.091
## S1.3 0.057     NA  0.048  0.061  0.076  0.084  0.013  0.074  0.037  0.041
## S1.4 0.319  0.595     NA -0.013  0.109 -0.029 -0.051 -0.071 -0.024  0.073
## S1.5 1.002  0.966  0.045     NA -0.043 -0.021 -0.035 -0.090  0.032  0.026
## S2.2 0.114  1.498  3.120  0.486     NA  0.020  0.019  0.077  0.074  0.107
## S2.3 0.382  1.827  0.215  0.115  0.109     NA -0.069 -0.041  0.069  0.094
## S2.4 0.319  0.048  0.669  0.314  0.095  1.242     NA -0.049 -0.024 -0.038
## S2.5 4.286  1.428  1.335  2.136  1.547  0.444  0.626     NA  0.039 -0.082
## S3.2 1.453  0.351  0.155  0.274  1.425  1.265  0.155  0.408     NA  0.089
## S3.3 2.158  0.439  1.401  0.174  2.979  2.336  0.387  1.744  2.059     NA
## S3.4 1.479  1.976  0.673  0.023  0.085  1.684  3.445  0.029  0.082  0.866
## S3.5 1.067  0.080  0.495  0.352  1.547  1.491  1.335  2.953  0.026  0.132
##        S3.4   S3.5
## S1.2 -0.075 -0.064
## S1.3  0.087 -0.017
## S1.4 -0.051  0.043
## S1.5  0.009 -0.037
## S2.2  0.018  0.077
## S2.3  0.080 -0.075
## S2.4 -0.115 -0.071
## S2.5  0.010 -0.106
## S3.2 -0.018 -0.010
## S3.3  0.057 -0.022
## S3.4     NA -0.088
## S3.5  2.012     NA

Other than the model fits and item fits, the “mirt” package also provides methods for calculating person fit statistics such as Zh statistics using the “personfit” function. In general, person fit statistics indicate how much a person’s responses on this test deviates from the the model prediction. See the “mirt” documentation and Drasgow, Levine, and Williams (1985) for further details.

head(personfit(uniDich.result1))

##      outfit    z.outfit     infit     z.infit         Zh
## 1 0.5429718  0.02890866 0.9234628 -0.06855284  0.3245494
## 2 0.3222275 -0.81981695 0.4792737 -1.50551326  1.2108896
## 3 1.3572362  0.68361016 1.6380112  1.45638093 -1.2704872
## 4 0.2944648 -0.60327684 0.4464912 -1.66830681  1.2602444
## 5 0.3693042 -0.15612325 0.6267169 -0.83751757  0.8026636
## 6 0.5580941 -0.53989285 0.8091663 -0.35965405  0.5450324

IRT Paramters

We can obtain the item parameters from the model. As aforementioned, for a Rasch model, all discrimination parameters are fixed to 1, while difficulty parameters are freely estimated. In the output, the second column (“a”) contains the discrimination parameters and the third column (b) contains the difficulty parameters.

In this example, we presented the IRT parameters using the conventional approach, such that a larger b parameter indicates higher difficulty of an item. For example, the second item, S1.3 (item size 3 in the 1st block), has a b = -0.94. This indicates that, according to the model estimation, a person with ability level that is 0.94 standard deviation below the average has 50% of chance to answer this item (S1.3) correctly.

# IRT parameters from the estimated model. For this example, we are obtaining simplified output without SEs/CIs (simplify = TRUE) for conventional IRT parameters (IRTpar = TRUE).
coef(uniDich.result1,simplify = TRUE, IRTpar = TRUE)$items

##      a          b g u
## S1.2 1 -3.0033639 0 1
## S1.3 1 -0.9388653 0 1
## S1.4 1  0.5864289 0 1
## S1.5 1  2.4373369 0 1
## S2.2 1 -2.6395715 0 1
## S2.3 1 -1.4247025 0 1
## S2.4 1  0.5864289 0 1
## S2.5 1  2.3201998 0 1
## S3.2 1 -2.3398444 0 1
## S3.3 1 -0.9845154 0 1
## S3.4 1  0.3420016 0 1
## S3.5 1  2.3201998 0 1

Visualizing the Item and Scale Characteristics

We can visualize corresponding item and scale characteristics from the model by a variety of plot methods in “mirt”. The plots presents how items and the entire scale relate to the latent trait across the scale.
We can start with the item trace plots for the 12 items. The item trace plots visualize the probability of responding “1” to an item as a function of \(\theta\). According to the item trace plot of this example, the 3 items with item size 2 (S1.2,S2.2,S3.2) are relatively easy items, in which subjects with average ability (\(\theta\) = 0) are estimated to have about 80% to 90% of chance to answer correctly. On the other hand, the 3 items with size 5 are relatively hard items, in which subjects with average ability are estimated to have about only 10% to 20% of chance to answer correctly.

# In the function we cam specify the range of theta we'd like to visualize on the x axis of the plots. In this example we set it to -4 to 4 (4 SDs below and above average).
plot(uniDich.result1, type = "trace", theta_lim = c(-4,4))

Other than the item trace plots, we can also look at the item information plots. Item information plots visualize how much “information” about the latent trait ability an item can provide. Conceptually, higher information implies less error of measure, and the peak of an item information curve is at the point of its b parameter. Thus, for easy items (such as the 3 items in the most left column below), little information are provided on subjects with high ability levels (because they will almost always answer correctly).

# We can specify the exact set of items we want to plot in the ploting function of mirt. Here we can also only visualize the 1st, 5th, and 9th item from the dataset by addin an argument "which.items = c(1,5,9)" in the function. This will make the function to only plot the 3 items with set size 2 in the task. Please feel free to give a try.
plot(uniDich.result1, type = "infotrace")

The “itemplot” function can provides more details regarding an item. This is an example that visualize the item trace plot of item 1 with confidence envelope.

itemplot(uniDich.result1, item = 1, type = "trace", CE = TRUE)

Lastly, we can plot the information curve for the entire test. This is based on the sum of all item information curves and indicate how much information a test can provide at different latent trait levels based on the model. As aforementioned, high information indicate less error (low SE) of measurement. An ideal (but impossible) test would have high test information at all levels of latent trait levels.

plot(uniDich.result1, type = "infoSE")

2PL Model

We can also estimate a 2PL model on the same binary data of rotation span task. In a 2PL model, not only the item difficulty parameters (bs) but also the item discrimination parameters (as) are estimated. Thus, a 2PL model assumes that different items vary in the ability to discriminate between persons with different latent trait levels.

uniDich.model2 <- mirt.model("rotation = 1 - 12")

uniDich.result2 <- mirt::mirt(dat1, uniDich.model2, itemtype = "2PL", SE = TRUE)

Model and Item Fits

Similarly, we can obtain corresponding statistics of the model such as model fit and item fit statistics. In this example, the overall model fit for the 2PL model is good.

M2(uniDich.result2)

##             M2 df         p RMSEA RMSEA_5   RMSEA_95      SRMSR      TLI CFI
## stats 40.90802 54 0.9054692     0       0 0.01662836 0.04004632 1.033223   1

Item fit statistics for this 2PL model indicate that the 2nd item (S1.3) may need further attention (significant S-X2 and large RMSEA).

itemfit(uniDich.result2)

##    item   S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
## 1  S1.2  1.607       6      0.000  0.952
## 2  S1.3 10.427       4      0.078  0.034
## 3  S1.4  6.922       5      0.038  0.227
## 4  S1.5  5.373       5      0.017  0.372
## 5  S2.2  4.646       5      0.000  0.461
## 6  S2.3  2.783       5      0.000  0.733
## 7  S2.4  3.550       6      0.000  0.737
## 8  S2.5  3.390       5      0.000  0.640
## 9  S3.2  1.839       5      0.000  0.871
## 10 S3.3  7.201       6      0.028  0.303
## 11 S3.4  6.146       6      0.010  0.407
## 12 S3.5  7.840       5      0.047  0.165

IRT Parameters

We can obtain the item parameters from the model. For a 2PL model, both the item discrimination parameters and the item difficulty parameters are freely estimated. Similar to the output of the Rasch model, the second column (“a”) contains the discrimination parameters and the third column (b) contains the difficulty parameters. We can see that, unlike the Rasch model, now every item has a unique discrimination parameter.

For a dichotomous 2PL model, the item discrimination parameters reflect how well an item could discriminate between persons with low and high ability/trait levels. Furthermore, the a parameter also reflects the magnitude to which an item is related to the latent trait measured by the scale. Thus, a low discrimination parameter usually indicates potential issues for an item comparing to the general scale.

coef(uniDich.result2,simplify = TRUE, IRTpar = TRUE)$items

##              a          b g u
## S1.2 0.8196465 -3.2455844 0 1
## S1.3 1.7771645 -0.6171063 0 1
## S1.4 1.3365861  0.4431670 0 1
## S1.5 1.2963837  1.9023919 0 1
## S2.2 1.7058414 -1.7589910 0 1
## S2.3 1.3696765 -1.0753956 0 1
## S2.4 0.8589407  0.5905375 0 1
## S2.5 0.9387174  2.2626112 0 1
## S3.2 1.4477736 -1.7033180 0 1
## S3.3 1.5741235 -0.6888211 0 1
## S3.4 1.2459076  0.2655880 0 1
## S3.5 0.9445384  2.2521152 0 1

Visualizing the Item and Scale Plots

Comparing to the Rasch model, the estimated a parameters in a 2PL model are also reflected in item trace plots, such that the differences in as are reflected by the changes in the steepness of the item trace curves. Higher as would be reflected as steeper item trace curves.

plot(uniDich.result2, type = "trace", theta_lim = c(-4,4))

The freely estimated discrimination parameters are also reflected in the item information plots. As we can see, comparing to the Rasch model, the peaks of information curves are varying across items in the 2PL model.

plot(uniDich.result2, type = "infotrace")

Model Specifications

The model specification function of “mirt” provides arguments for further constraints in an IRT model and can be used for testing specific assumptions regarding the item characteristics.
For example, in the rotation span task, items with the exact same set size are designed in the exact same way. Thus, we consider the items with the same set size equivalent in their ability to discriminate persons with different ability levels. To estimate this model, we can specify the constraints in the model specification function. As is presented, in the function we specify an equal a parameter for items 1, 5, & 9, which are labeled “S1.2”, “S2.2”, and “S3.2” in the dataset (these are the 3 items with set size 2); another equal a for items 2, 6, & 1; another for items 3, 7, and 11; and another for items 4, 8, and 12.

uniDich.model3 <- mirt.model("rotation = 1 - 12
                             CONSTRAIN = (1,5,9,a1), (2,6,10,a1),(3,7,11,a1),(4,8,12,a1)")

uniDich.result3 <- mirt::mirt(dat1, uniDich.model3, itemtype = "2PL", SE = TRUE)

The specification in constraints is reflected in the IRT parameters from this model. As we can observe, in the IRT parameters output, items with the same set sizes are estimated to have the exact same a parameters. For all items with size 2, a = 1.31, and for all items with size 3, a = 1.55, etc. On the other hand, the b parameters are still freely estimated regardless of the item size.

coef(uniDich.result3,simplify = TRUE, IRTpar = TRUE)$items

##             a          b g u
## S1.2 1.314847 -2.3120591 0 1
## S1.3 1.551951 -0.6626354 0 1
## S1.4 1.127870  0.4902232 0 1
## S1.5 1.036344  2.2120724 0 1
## S2.2 1.314847 -2.0337955 0 1
## S2.3 1.551951 -1.0029799 0 1
## S2.4 1.127870  0.4902232 0 1
## S2.5 1.036344  2.1036240 0 1
## S3.2 1.314847 -1.8044209 0 1
## S3.3 1.551951 -0.6946542 0 1
## S3.4 1.127870  0.2815835 0 1
## S3.5 1.036344  2.1036240 0 1

We can also do model comparisons for nested models with different constraints. For example, we can test the difference between this constrained model and the previous 2PL model without any constraints on discrimination. This is similar to a model comparison based on chi-squared statistics for nested SEM models. As we can see, results indicate that the two models are not significantly different from each other, \(\Delta\chi^2\)(8) = 8.68, p = .37.

anova(uniDich.result2,uniDich.result3)

##                      AIC    SABIC       HQ      BIC    logLik     X2 df   p
## uniDich.result2 2948.644 2958.194 2983.065 3034.285 -1450.322              
## uniDich.result3 2941.329 2947.695 2964.276 2998.422 -1454.664 -8.684 -8 NaN

Unidimensional Polytomous IRT Model

In the previous section we have conducted dichotomous IRT analyses on the rotation span task dataset with binary responses. However, the initial rotation span dataset consist of numbers of correctly recalled elements for each item. In other words, each item actually has more than two possible response categories that are at least ordinal. For example, for an item with set size 2 (2 elements in the item), there are 3 possible response outcomes: 0, 1, and 2. Thus, we could fit and assess a polytomous IRT model to this type of measures, such as partial-scored tests and Likert-type surveys.

dat2 <- as.matrix(wmirot[,-1])
head(dat2)

##      S1.2 S1.3 S1.4 S1.5 S2.2 S2.3 S2.4 S2.5 S3.2 S3.3 S3.4 S3.5
## [1,]    2    1    0    0    0    3    1    0    1    1    0    0
## [2,]    2    2    1    1    2    3    2    2    2    2    1    1
## [3,]    2    1    4    1    2    3    4    1    1    2    0    3
## [4,]    2    2    3    1    2    0    1    1    2    2    3    4
## [5,]    2    3    4    5    2    3    4    4    2    3    4    2
## [6,]    2    3    0    2    2    3    4    3    2    1    2    1

Generalized Partial Credit Model

In this section, we will apply the generalized partial credit model (GPCM; Muraki, 1992) to the rotation span data. As a polytomous model, GPCM estimates one item threshold parameter for each response category in an item instead of one difficulty parameter for an item. Further more, GPCM assumes an unique item discrimination parameter for each item instead of assuming a unitary reliability across items (like the Rasch model).

unipoly.model1 <- mirt.model("rotation = 1 - 12")

unipoly.result1 <- mirt::mirt(dat2, uniDich.model2, itemtype = "gpcm", SE = TRUE)

Model and Item Fits

Similarly, we can obtain corresponding statistics of the model such as model fit and item fit statistics. In this example, the overall model fit and all item fits for the GPCM model are good.

M2(unipoly.result1)

##             M2 df         p RMSEA RMSEA_5   RMSEA_95      SRMSR      TLI CFI
## stats 23.66605 24 0.4808204     0       0 0.04927329 0.04771738 1.005053   1

itemfit(unipoly.result1)

##    item   S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
## 1  S1.2 15.329      11      0.039  0.168
## 2  S1.3 46.224      32      0.041  0.050
## 3  S1.4 43.506      48      0.000  0.657
## 4  S1.5 44.058      58      0.000  0.912
## 5  S2.2 20.725      13      0.048  0.079
## 6  S2.3 30.299      26      0.025  0.255
## 7  S2.4 48.715      50      0.000  0.525
## 8  S2.5 71.664      61      0.026  0.165
## 9  S3.2 13.519      17      0.000  0.701
## 10 S3.3 20.588      32      0.000  0.940
## 11 S3.4 52.075      51      0.009  0.432
## 12 S3.5 63.890      63      0.007  0.445

IRT Parameters

For a GPCM model, the item discrimination parameters and the item threshold parameters are freely estimated. In a GPCM model, the item threshold parameter is defined as the trait level in which one has an equal probability of choosing the kth response category over the k-1th category in an item. When choosing between the kth and the k-1th category, subjects with trait levels higher than that threshold are more likely to approach the kth, while subjects with trait levels lower than that threshold are more likely to approach the k-1th.

coef(unipoly.result1,simplify = TRUE, IRTpars = TRUE)$items

##              a         b1          b2         b3        b4          b5
## S1.2 0.6354780 -2.4238753 -4.50115962         NA        NA          NA
## S1.3 0.8367055 -1.5716066 -0.89123631 -1.8001978        NA          NA
## S1.4 0.5989767 -1.8187952 -0.50303114  0.5399410 -1.379714          NA
## S1.5 0.4660780 -0.7725926 -0.02659485  0.5368132  1.745108  0.07050096
## S2.2 1.0176875 -1.8131900 -2.77011850         NA        NA          NA
## S2.3 0.8606748 -2.3689773 -0.88851301 -2.2413670        NA          NA
## S2.4 0.4985639 -1.6434258 -0.70470153 -0.3802990 -1.060266          NA
## S2.5 0.4158617 -0.5284300 -1.00120923  1.5317726  1.243526 -0.09643630
## S3.2 0.8508984 -1.3638275 -3.01408652         NA        NA          NA
## S3.3 0.8038394 -1.7838070 -1.03577722 -1.8430426        NA          NA
## S3.4 0.5793661 -0.6192944 -0.94635296  0.0811653 -1.540936          NA
## S3.5 0.4046533 -0.5014941 -0.68390425  0.3561937  1.278277  0.42457494

In this example, the function utilizes the conventional IRT parameterization. In the conventional parameterization, for an item of size p, GPCM estimates p item threshold parameters for each of the categories (from “b_1” for partial scores of 0 and 1 to “b_p” for partial scores p-1 and p), and 1 item discrimination parameter for the item. The second column (“a_1”) contains the discrimination parameters and the later columns (“b_1” to “b_5”) contain all the threshold parameters.

Visualizing the Item and Scale Plots

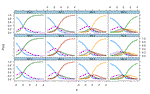
Similar to the dichotomous 2PL model, the estimated a parameters in a GPCM model are reflected in item trace plots, such that the differences in as are reflected by the changes in the steepness of the item trace curves. Higher as would be reflected as steeper item trace curves. On the other hand, the estimated b parameters in a GPCM model are reflected as (x-axis values for) the adjacent points between trace curves for different categories. For example, for Item S3.2, the current GPCM model estimated two threshold parameters: b1 = -1.36 (the adjacent point between curve P1 and P2) and b2 = -3.01 (the adjacent point between curve P2 and P3).

plot(unipoly.result1, type = "trace", theta_lim = c(-4,4))

Similar to the dichotomous 2PL model, the freely estimated discrimination parameters are also reflected in the item information plots.

plot(unipoly.result1, type = "infotrace")

Individual Scoring

Based on an estimated model, we can also estimate the individual latent trait scores. Conceptually, the estimated latent trait scores are similar to factor scores estimated in CFAs.

est.theta <- as.data.frame(fscores(unipoly.result1))
head(est.theta)

##     rotation
## 1 -1.9429664
## 2 -0.7051405
## 3 -0.5498356
## 4 -0.6928339
## 5  1.4039574
## 6 -0.3787596

est.theta %>% 
  ggplot(aes(x=rotation)) +
    geom_histogram(aes(y=..density..),
                   binwidth=.1,
                   colour="black", fill="white") +
    geom_density(alpha=.2, fill="aquamarine2")

## Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(density)` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.